Variance is an important concept in the theory of probability and statistics. Variance is loosely defined as the measure of how far a set of numbers are spread from their average or mean value. In other words, it measures and tells you how spread your data in. The symbol of variance is . Calculating variance while doing a problem on statistics is a bit tricky but it is just remembering few formulae and putting the right numbers in it.
So here we explain step by step on how to calculate variance when the data set is of a sample and of a population.
Calculating Variance of a Sample
-
- The first step is to write the sample data set given to you. While doing a research, statisticians usually don’t get data from the entire population, so they use a small subset of the entire population and then perform statistics.
- The next step is to write down the variance formula. The formula for calculating variance is as follows:
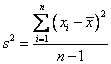
is the variance. Variance is always measured in squared units.- represents a term in your data set.
- ∑, meaning “sum,” tells you to calculate the following terms for each value of , then add them together.
- xÌ… is the mean of the sample.
- n is the number of data points.
- If you don’t have your mean or x̅ calculated then you can use this technique to calculate mean. Add all the data points together and then divide them by number of data points or n.
- Now subtract mean from each data point or . Each answer tells you how much that particular number is deviated from the mean. In other words, how far that number is from the mean.
- The next step is to square each result that you got from the above step. And then add all these squared values that you got.
- The last step is to divide the value that you obtained above by n-1 where n is number of data points. And the answer that you get is the variance of the sample.
represents a term in your data set.- Calculating Variance of a Population
- Write down the population data set given to you. In some cases of statistics, it is easy to find the data from the entire population and hence the statisticians use data from the population for their research.
- Write down the formula to calculate variance of population data. The formula for calculating variance is as follows:
where,
- σis equal to population variance. This is a lower-case sigma, squared. Variance is measured in squared units.
- is represents a term in your data set.
- The terms inside ∑ will be calculated for each value of , then summed.
- μ is the population mean.
- N is the number of data points in the population.
- The next step is to calculate mean or μ of the population. To find the mean, add all the data points together and divide by the total number of data points.
- Now subtract each data point from the mean that you have obtained from the above step i.e.
- Now square all the values that you have obtained from the above step and add them all together.
- The last step is to divide the value that you have obtained by N or the number of data points in the population.
